© 2021 Totem Publisher, Inc. All rights reserved.
Introduction
Humans are gifted with the amazing ability to experience the ambience of nature through their sensory organs. Technology has enabled us to capture the ambience in the form of signals and allowed humans to reproduce it as per their convenience. Particularly, reproducing ambient sound captured in a closed room environment needs thorough understanding of the sound interaction with the environment. These interactions can be characterized using Room Impulse Responses (RIR). In the past few decades, many RIR databases have been developed in order to understand the interaction of sound and reproduce the ambience of closed room environments [1-2]. Broadly, a RIR contains three components: direct, early and late components [3]. While it is possible to extract some of the crucial room acoustic parameters using an Omni-RIR, it is impossible to extract the spatial information (azimuth and elevation) of the direct and early components. In order to obtain the spatial information, an array of spherically distributed microphone is needed [4]. One such arrangement is called a B-Format microphone with tetrahedral arrangement [5]. RIRs are measured using B-Format and capture spatial variations, and therefore, it is possible to extract the spatial information of direct and early reflections.
Recently, a method to completely parameterize these components was developed, called the Reverberant Spatial Audio Object (RSAO) [6-12]. The Reverberant Spatial Audio Object approach exploits the spatial arrangements of the B-Format microphone to extract these parameters. Direct component parameters of RSAO consists of levels, onset times and direction of the direct signal [13-17]. Parameters of early components consists of number of reflections considered, levels and onset times of each reflection, and the spectral characteristics of each reflection. Late component is divided into nine octave sub-bands in the audio frequency spectrum parameterized as exponential decay coefficients. These parameters capture the behavior of direct, early and late reflections. While these parameters are computable using RSAO, the lack of any ground truth makes it harder to test the accuracy of the parameters. In this work, the authors attempt to make an error analysis on the extracted parameters. Particularly, parameters for which a clear relation can be established with the physical dimensions of the room, and it is analyzed using the Polynomial Curve Fitting [18] to generalize the sample parameters obtained.
The rest of the paper is organized as follows. Section 2 contains the discussion about early reflection parameter analysis of both simulated models and the Reverberant Spatial Audio Object. Polynomial curve fitting is performed for both elevation angles and onset times across distances. Section 3 discusses the result analysis of the early parameters with polynomial curve fitting. Section 4 concludes the paper.
Early Reflection Parameter Analysis using Reverberant Spatial Audio Object and Simulated Models
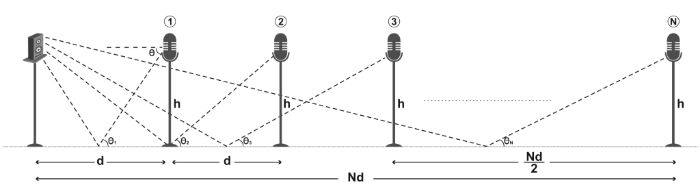
Early reflections are the signals that arrive to the microphones reflected from the surfaces of the room. Using techniques like Reverberant Spatial Audio Object, it is possible to compute various parameters from the signals measured from the B-Format microphone. More importantly, the spatial arrangements of B-Format mics enable the computation of the direction of the reflections using beamforming techniques. However, it is a challenging task to identify nonspurious reflections that have a one-to-one mapping with the walls of the rooms. This is evident due to the fact that there is no systematic pattern in most of the reflection directions when the parameters are computed for various source receiver distances. The only early reflections that are able to exhibit a mapping is the ground and floor reflections [19]. However, there still exists inconsistencies in the computed directions when compared against simulated models like Image source methods. Consider B-Format Room Impulse Responses measured for N different source receiver distances in a classroom like environment as shown in Figure 1. The N microphone positions are arranged in a linear fashion uniformly spaced with a separation of distance d. Also assume the separation between the source and the first B-format microphone position as d. Various early reflection parameters extracted using measured B-Format Room Impulse Responses and the simulated models are discussed below.
Figure 1.
Figure 1.
Angular variation of the sound reflections from the ground for microphones located at various distances.
2.1. Computation of Ground Reflection Elevations using Simulated Room Impulse Response and Measured B-Format Room Impulse Response
The ground reflections are indicated as straight lines or rays similar to the assumption made in the image source method
[20-21]. The first early reflection exhibits similar distance before and after ground reflection as shown in Figure 1. The angle subtended by the first reflection with the ground to the nth microphone is given by:
The angle subtended by the reflection with the ground is the same as the angle subtended by the microphone with the horizontal axis (computed in RSAO) as shown in Figure 1 (alternate angles). It can be noted that the tangent of the angle is inversely proportional to the distance between source and the microphone. Although this relation is based on the assumption that the sound propagates as rays, this relation provides insights into how the reflections should change with respect to distance. In this work, the authors consider this as the Simulated Model and take this as a reference to analyze the angular variation of the first reflection extracted through B-Format RIRs. This analysis is performed by modelling elevation angles of ground reflection obtained for measured B-Format RIRs using a polynomial curve fitting.
2.2. Computation of Ground Reflection Onset Times using Simulated RIR and Measured B-Format RIR
The time required for the signal to reach from source to receiver is called onset time. For a Room Impulse Response signal measured in a room, direct signal has the least onset time. The next dominant component is the ground reflection assuming that the ground is closer than the walls and ceiling. Assuming an ideal case, the sound reflected from the ground travels a time duration given by:
Where c=343m/s is the speed of sound in air and tn is the onset time of the ground reflection to reach the sound from the source to the nth microphone. Onset time is also obtained from the B-Format signals using the RSAO method. Reverberant Spatial Audio Object utilizes the Dypsa algorithm [22] to identify the ground reflection components and its onset time. Ground reflections obtained by both methods, first using Reverberant Spatial Audio Object and later using Equation 3, are analyzed using a polynomial curve fitting in this work.
2.3. Polynomial Curve Fitting based Early Parameter Analysis
Consider M is the model order and pn is the early parameter from the ground captured by the B-format mic at the nth position. Then, the Mth order curve fitting model is given as:
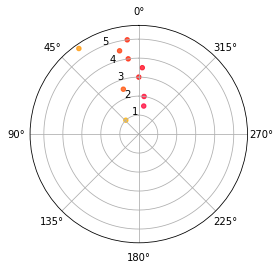
Figure. 2.
Figure. 2.
Azimuthal angle variation for various source receiver distances
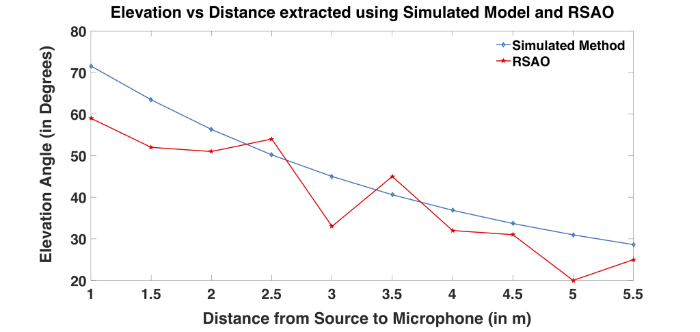
Figure. 3.
Figure. 3.
Elevation angle obtained using Simulated Model and RSAO computed for various source receiver distances
Where 𝜃𝑛 is the elevation angle of the ground reflection. tn is the onset time to the nth microphone. K0, k1, … kN are polynomial quotients.
This model is used in this work for two purposes. First, to have a similar representation for both simulated and measured early parameters that are independent of the number of sample positions. Second, to predict the elevation angles for the non -measured directions. The solution to the polynomial curve fitting problem for N > M can be obtained using the least squares as follows.
The results obtained for both these analyses are discussed in Section 3.
Result Analysis
In this section, the database used for RSAO parameter analysis is first discussed. Subsequently, results obtained for the ground reflection elevations, azimuths and onset times for both simulated and measured RIRs are presented. Finally, the polynomial curve fitting performance is also discussed.
3.1. B-Format RIR Database
There are very few databases available with B-Format RIRs measurements that are systematically measured for various distances [5,23]. One such database is the QMUL database [5]. This database was developed for a grid of sampling points for three different rooms: Classroom, Octagon, and Great Hall. In this work, the Classroom B-Format RIR database is used for extracting RSAO parameters.
3.2. Performance Analysis of Ground Reflection Directions for Simulated and RSAO Approaches
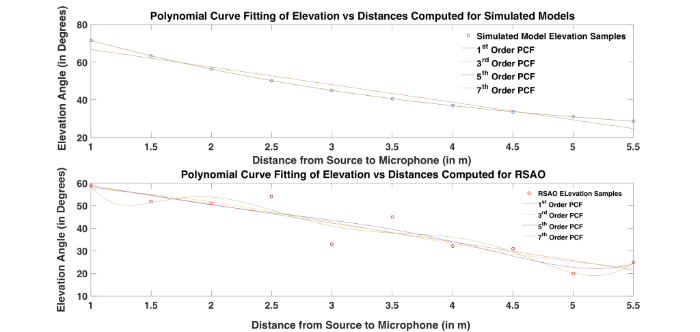
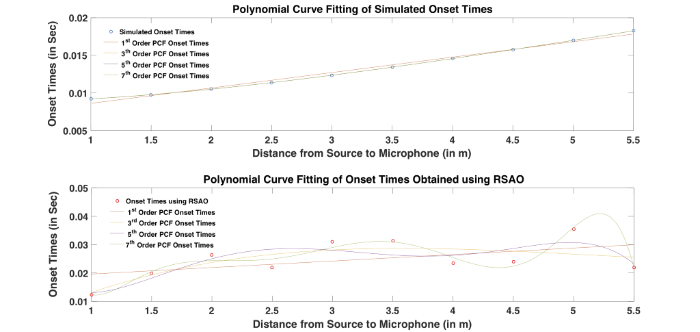
A ground reflection direction is represented as an ordered pair of azimuth and elevation angles. As the sound source is in line with the microphone, ideally the azimuthal angle should be zero. But when extracted from the measurement, the computed azimuth varies as shown in Figure 2. It hovers around zero degrees. Elevation angle variation is very important in analyzing the ground reflections. As shown in Figure 1, the elevation angle decreases with an increase in distance between source and microphone. The angle subtended by the microphone with the horizontal axis (computed in RSAO) is the same as the angle subtended by the reflection with the ground (computed in Simulation model using Equation 1). The elevation angle computed through RSAO and the angle computed using Equation 1 are shown in Figure 3. As the latter exhibits a closed form expression, the monotonic nature of the curve can be seen in Figure 3. However, the measured elevations have fluctuations that make the task of identifying parameters for non-measured directions difficult. The solution explored in this work for this problem is to apply a polynomial curve fitting. Figure 4 illustrates the elevation angles as scattered points obtained for simulated (top) and RSAO (bottom) for 10 different distances used in the Classroom database. It also illustrates the polynomial curve fitting of order 1, 3, 5, and 7 performed on the 10 sampling points. Because of the monotonic variation of elevation angle for the simulated model, the lower orders were able to successfully model the sampling points. However, the elevation angles obtained using RSAO need a higher order for proper generalization of sampling points. It can be seen that increasing the order attempts to fit the data. However, PCF orders greater than 5 creates over-fitting of the data, which can be observed from
Figure 4. Fixing a particular order will enable the capture of the ground reflection elevation angles for non-measured directions.
Figure. 4.
Figure. 4.
Elevation angles obtained by simulated and RSAO for 10 different distances used in the Classroom Database. Polynomial curve fitting of order 1, 3, 5, and 7 performed on the 10 samples.
Figure 5.
Figure 5.
Onset times obtained by simulated and RSAO for 10 different distances used in the Classroom Database. Polynomial curve fitting of order 1, 3, 5, and 7 performed on the 10 samples.
3.3. Performance Analysis of Onset Times for Simulated and RSAO Approaches
Onset times computed for 10 sampling positions using the simulated model through Equation 3 and using RSAO is presented in Figure 5. Similar to elevation angles discussed in the previous section, onset times also exhibit a monotonic curve for the simulated model because of the closed form expression. However, the variation of onset times is more for measured signals obtained through RSAO. Polynomial curve fitting helps generalize the sampling points and thereby enables the capture of the onset times for non-measured directions. It has to be noted that onset times obtained through RSAO are relative to the direct signal time instant. Hence, the direct signal onset time is added to the onset times obtained through RSAO to calculate the total onset time of the ground reflection. In this manner, polynomial curve fitting helps identify the early parameters for non-measured directions.
Conclusion
Early parameter variations are more monotonic in simulated models as compared to the parameters extracted from Reverberant Spatial Audio Object (RSAO). Polynomial curve fitting of RSAO parameters for ground reflections needs a higher model order as compared to the simulated model for equivalent parameters. The polynomial curve fitting method is able to generalize the observed sample parameters and enable the computation of the parameters for non-measured directions. This work can be extended in multiple ways. It can be used to measure a slightly denser grid of B-Format RIRs in a closed room so that the error analysis on the early parameters for non-measured directions can be performed. The second extension can focus on other early parameters apart from spatial directions and onset time.
Reference
Simultaneous measurement of impulse response and distortion with a swept-sine technique
Acoustic reflector localization: novel image source reversion and direct localization methods
Object-based reverberation for spatial audio
Object-based audio reproduction and the audio scene description format
Object-based audio: Opportunities for improved listening experience and increased listener involvement
An Introduction to Statistical Learning with Applications in R
Image method for efficiently simulating small‐room acoustics
Prediction of energy decay in room impulse responses simulated with an image-source model