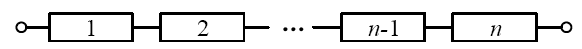1. Introduction
The modern informationalized joint warfare with system antagonism as the main form has the characteristics of quick war process, large equipment resource loss, and wide space-time span. Therefore, the scientific evaluation and prediction of the reliability status of ESoS are of great significance to the formulation of operation missions and support plans, the establishment of a matching, sound, and sensitive integrated support system, andthe winning of an informationalized war. The reliability modeling of ESoS is an important part of the equipment integrated support work and one of the basic missions of optimizing the equipment support capability and bringing the operation effectiveness of the ESoS into full play [1-3].
At present, most of the research on reliability modeling focuses on single-equipment or equipment systems. The traditional modeling methods include the reliability block diagram (RBD), the fault tree (FT), and Markov chains (MC). The purpose is to identify the equipment failure mode and achieve the level of system reliability, thereby saving maintenance support costs. For example, Sun established the evaluation model of the availability of serial-parallel hybrid RBDs for heterogeneous systems using the reliability block diagram and compared them with the Markov process method [4]. Reference [5] applied the FT method to evaluate the reliability of subsea tank equipment. Most of the research on the modeling of equipment reliability focuses on simulation methods such as Petri nets. For example, Jiang modeled the reliability of equipment system based on DoDAF framework and time Petri net flow analysis [6]. Qiao conducted a systematic study on the mission reliability modeling of the equipment system based on the extended object Petri net method and developed modeling software[7].
With the improvement of the informatization level of weapon and equipment, the expansion of the battlefield dimension and the progress of combat methods, equipment, and the relationships between equipment and equipment systems are very close. Therefore, it is necessary to establish a SoS-level reliability model from the perspective of mission reliability (MR). The mission reliability evaluation of the ESoS is an important aspect of the analysis of ESoS supportability.
Through the analysis of the research status of the ESoS mission reliability modeling, it is found that there are mainly two problems:
(1) Reliability modeling research mainly focuses on single equipment or equipment systems, and research on the composition of large-scale ESoS with complex systems is limited.
(2) When the component system within the SoS fails and quits, the SoS will experience a degree of performance degradation that is not an absolute state as perfect or complete failure. Therefore, in the research on reliability modeling, the basic logical structure of series-parallel and redundant structure cannot accurately describe this feature of EsoS [8].
In view of the above problems, this article considered the more common situation of setting a large amount of redundant combat equipment inside the functional system of the ESoS when performing the mission. In the single-phase mission profile background, the typical army equipment system was taken as the research object, the characteristics of the ESoS structure were analyzed, and the reliability of the SoS mission was used as the evaluation index. A mission reliability model for ESoS was constructed, and methods for solving the same and different equipment failure probabilities were proposed. A case study was to verify the rationality and effectiveness of the model [9-10].
2. Description of Equipment System of Systems
Define the equipment system of systems (ESoS) as an integrated whole set of equipment of various types that are functionally related to each other in a dynamic and uncertain environment.
2.1. Structure ofESoS
ESoS is coupled by various types of equipment, so its hierarchical structure is very obvious.
2.1.1. Functional Structure
According to the corresponding relationship between the functions of the various levels and the mission of the ESoS, the hierarchical description method can be used to divide the ESoS into system layer, system/platform layer, and equipment layer.
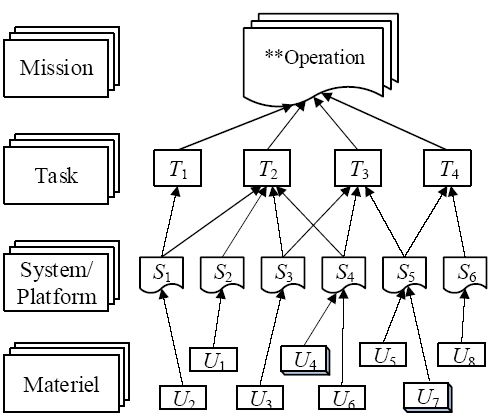
In the usual sense, related equipment/devices are first assembled to form a kind of system or platform and then, driven by the mission, each equipment system/platform is integrated into ESoS with emerging and evolutionary capabilities through interconnection and interoperability. For instance, the air defense missile system consists of missiles, command and control equipment, launch guidance equipment, and other auxiliary equipment. As shown in Figure 1, a combat mission “**Operation” can be divided into multiple mission phases T1, T2,··$\cdot$ based on temporal logic. Each phase corresponds to one or more functional systems S1, S2, ···. Each functional system consists of one or more equipment units U1, U2, ···.
Figure 1.
Figure 1.
ESoS function concept diagram
A typical army ESoS consists of an integrated electronic information system (command and control system), multiple weapons and equipment systems or platforms (such as early warning detection systems, fire strike systems, etc.), and matched support systems.
2.1.2. Implementation Structure
According to the implementation in the combat process, ESoS can be divided into equipment combat units and basic equipment combat units.
Armed combat units are combat unit equipment capable of independently carrying out combat missions within a certain range. They consist of basic equipment combat units, which are the smallest military units that can independently perform combat and training missions. Equipment combat units are usually composed of different functions, types, varieties, and series of equipment according to a certain degree of matching, linking and proportion relations, and levels [11-12].
According to the current international practice of army operations, the basic operational units of the army’s basic equipment are generally linked or formed as units, with infantry companies, artillery companies, and security and military detachment units. The combat units are generally based on battalion or squadron and infantry units. On this basis, the equipment system can be regarded as consisting of equipment under the jurisdiction of brigade and brigade units.
Take the US Army’s new Stryker brigade as an example. There are three infantry battalions under the jurisdiction of the camp. Each battalion has three infantry companies under its command (each equipped with 12 combat vehicles),one artillery battalion under the jurisdiction of a mobile gun company (equipped with nineself-propelled artilleries), and one artillery company (equipped with 18 howitzers).In addition, the brigade is an anti-tank company (equipped with nine anti-tank guided missile launchers) and an armored reconnaissance squadron (equipped with 42 armored reconnaissance vehicles). There are also many directly-owned protection teams such as the headquarters, health company, maintenance and military supplies company, communications company, and engineering company.
2.2. Characteristics of ESoS
(1) Structural complexity
The equipment system of systems contains a large number of various types of equipment. The types, informatization degrees, service time, failure mode, and failure rate of equipment all vary greatly.
(2) Loosely coupled relationship between the constituent systems
The system components within the ESoS are loosely coupled, and the reliability relationship between equipment and equipment systems is not relevant. If the traditional method is used for ESoS reliability research, the conclusions obtained will have no practical significance.
(3) The composition system has a specific function
Composition systems usually have specific capabilities. Multiple systems create synergies in the completion of missions through communication and interoperability.
In summary, the SoS does not have a definite reliability logical relationship simply from the structural point of view. However, composition systems are coupled together through system missions. Therefore, the mission reliability of ESoS can be explored from the perspective of the mission reliability.
3. Mission Reliability Modeling forESoS
3.1. Traditional Structure of System
The traditional structure of the system can be divided into series structure, parallel structure, and voting structure according to the reliability logic relationship.
(1) The series structure means that any component in the system fails and the system will fail. Its reliability block diagram is shown in Figure 2. The reliability model of the series structure system is
Figure 2.
Figure 2.
Reliability block diagram of series structure
where $R\left( t \right)$ is the reliability of the series structure system and ${{R}_{i}}\left( t \right)$ is the reliability of the ith component that constitutes the series structure system.
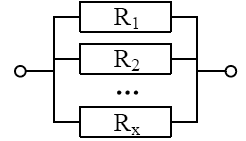
(2) The parallel structure is a system in which only one component can work normally and the system is in a normal state. At the same time, only if all components fail does the system fail. Its reliability block diagram is shown in Figure 3. When the reliability of the parallel components is different, the reliability model of the parallel structure system is
Figure 3.
Figure 3.
Reliability block diagram of parallel structure
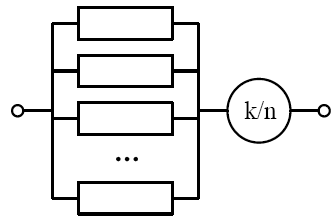
(3) The voting structure, also called the $k/n(G)$ structure, consists of n identical components. When at least k components work normally, the system is in normal working condition. When the number of failed components in the system is greater than $(n-k)$, the system is judged to be invalid. The parallel structure is a special voting structure. The reliability block diagram is shown in Figure 4. The reliability model of the voting structure system is
Figure 4.
Figure 4.
Reliability block diagram of vote structure
The logical structure of traditional systems is mostly composed of the above three basic logical structures. However, for the SoS, the primary feature is the management and operational independence of the constituent systems. The relationship between the systems is loosely coupled. When the system exits after a failure, it will not cause other systems to fail. This phenomenon is similar to the parallel structure, but the failure of the constituent system will usually result in the decline of the system performance. Therefore, systems in SoS are not connected in parallel or in series, and the voting structure cannot accurately describe this phenomenon. Therefore, the concept of the weighted parallel structure is introduced in this paper.
3.2. Mission Reliability of ESoS based on Weighted Parallel Structure
3.2.1. Weighted Parallel Structure of SoS
The weighted parallel structure describes the reliability logical relationship of the internal systems in SoS. In this structure, the reliability of the entire SoS is obtained by adding systems’ reliability through certain weights. The weights are mission proportions undertaken by each system. If one or multiple systems fail during the mission, the accomplishment degree of the SoS mission will be reduced along with system failure, resulting in a decline in SoS mission reliability.
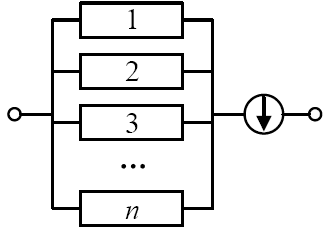
There are two kinds of weighted parallel structure according to the components: the same unit structure and the different unit structure. The SoS is formed by several systems with unique capabilities. In other words, the structure of SoS generally refers to the different unit types. The reliability block diagram of the power structure is shown in Figure 5.
Figure 5.
Figure 5.
Reliability block diagram of weighted parallel structure
3.2.2. Determination of System Weight
The weight of a system in SoS refers to the system’s share in the SoS mission, which reflects the system’s contribution to the SoS capabilities. Therefore, we use contribution-to-SoS of a system as its weight.
The definition of the contribution-to-SoS given by Luo is the extent to which the system’s combat capability has changed after the equipment or equipment system is incorporated into the equipment SoS [13].
Existing evaluation methods of contribution-to-SoS are based on CAS, Structural Equation Modeling (SEM), exploratory analysis, and complex networks. Reference [13] considers gathering mission contribution, capability contribution, structural contribution, and evolution contribution to aggregate and calculate the contribution-to-SoS.
In order to simplify the calculation, this article determines the contribution-to-SoS of each system using the Delphi method, which is based on expert scores and statistical corrections.The specific process is as follows:
Step 1 Determination of the scoring expert. Select experts with rich experience in the field, and lay a solid foundation for the accuracy of evaluation.
Step 2 Collection of expert scores. Give all experts questions to evaluate, that is, the degree of the impact on ESoS after one functional system fails to exit the SoS. Then, define the scoring rules. Finally, collect the score results.
Step 3 Normalization. First, calculate the arithmetic mean value of the expert scores for each system. Then, normalize the arithmetic mean values of all systems.
The results obtained so far are the contribution-to-SoS of each system, that is, the weight of system reliability in the ESoS.
3.2.3. Mission Reliability Model for SoS
Assume that the ESoS is coupled by n systems with different functions. ${{S}_{i}}$ and ${{\overline{S}}_{i}}$ represent respectively that system i ($i=1, 2,\cdots , n$) is in a reliable working state and a failure state. Assume that ${{E}_{i}}$ represents the proportion of system i that bears the system mission ($0<{{E}_{i}}<1$), which is the weight coefficient. Therefore, when all systems are in good condition, the reliable working status ${{S}_{S}}$ of SoS can be expressed as
If one system fails in the SoS, the reliability working status ${{S}_{S}}$ can be expressed as
Similarly, when there are two systems i and j in the SoS failure, the reliability working status ${{S}_{S}}$ of SoS can be expressed as
By analogy, when there are k systems failing, the reliability working status ${{S}_{S}}$ can be expressed as
Since the above states do not intersect with each other, all the states are summed to obtain the reliability working state ${{S}_{S}}$ of SoS in any case, which is
To obtain the state probability on both sides of Equation(8), the reliability ${{R}_{S}}$ of the SoS is
In practical applications, there are many component systems of the ESoS, and the calculation on the right side of Equation(9) will be more complicated. Then, it is not possible to obtain the equation results quickly even with computer software. Therefore, an approximate algorithm is developed to ensure the calculation results and accelerate the calculation speed.
According to the definition, the weighted parallel structure adds weights on the basis of the parallel redundant structure. Therefore, the reliability of the ESoS is approximated by the product of the reliability of parallel structure and the sum of the weighted reliability of each component system, i.e.:
3.3. Model Solution
3.3.1. Parameter definition
For the convenience of model description, the following parameters are defined:
i) M is the number of functional systems coupled to form an ESoS.
ii) ${{n}_{i}}$ is the number of identical equipment that make up system i; at system level, each function system is set to a redundant system such as infantry company and artillery company to ensure reliable operation.
iii) ${{k}_{i}}$ is the number of intact equipment needed to keep the system working properly. The equipment failure events are independent of each other.
iv) ${{m}_{i}}={{n}_{i}}-{{k}_{i}}+1$ is the number of equipment failures that cause the system to fail. Once the number of equipment failures reaches this value, it is determined that the functional system has exited the system.
3.3.2. Solution
The probability of equipment failure is the same in the system, that is, the reliability of each equipment in system iis ${{p}_{i}}$, the degree of unreliability is ${{q}_{i}}$, and ${{q}_{i}}=1-{{p}_{i}}$. Since the system is $k/n(G)$ redundant system, the system reliability can be obtained from Equation(3):
Meanwhile, when the failure probability of equipment in the system is different, the equipment failure number j in system i before the end of the mission is recorded as the system state ${{X}_{i, j}}$, and then ${{X}_{i, j}}=j=0, 1, 2,\cdots ,{{m}_{i}}$. From the full probability formula, the state probability ${{Z}_{i, j}}$ of system i is
Assuming that the reliability of the system equipment is ${{R}_{i, a}}$, in particular, when $j=0$, we have
Then, the reliability ${{R}_{i}}$ of system i is
Equations(9) and (10) are the calculation formulas for SoS reliability, and Equations(11) and (14) are the reliability of the equipment redundancy system with the same equipment failure rate and different conditions. Combining the three equations can obtain the SoSreliability ${{R}_{S}}$.
Through the above model, the reliability of ESoS with weighted parallel structure without considering the maintenance guarantee can be obtained.
The following is a case study of the US Stryker brigade in 1.1.2 to illustrate the usability of the established model.
4. Case Study
4.1. Background
The basic combat unit of the US Army Stryker brigade consists of nine infantry companies, one artillery company, one self-propelled artillery company, one anti-tank company, and one armored reconnaissance battalion. They use step vehicles, howitzers, self-propelled artilleries, anti-tank guided missile launch vehicles, and armored reconnaissance vehicles as five kinds of equipment system platforms. They formed a number of $k/n(G)$ redundant systems with different capabilities and became part of the Stryker brigade ESoS.
Due to equipment failures and enemy fire strikes, equipment has failed one after another. In order to simplify the problem and highlight the key, it is assumed that the failure rate of the equipment in the equipment system is the same. The maintenance is not considered during the execution of the mission. Once the equipment fails, it will remain in a fault state. When the rate of equipment failures in the system exceeds 2/3, the system is considered to be ineffective, which is ${{m}_{i}}=\left[ \frac{2}{3}{{n}_{i}} \right]$.
Table 1. Fight materiel in Stryker brigade
| Troop | Materiel | Quantity | Failure threshold |
|---|---|---|---|
| Infantry company 1-9 | Step vehicle | 12/company | 8 |
| Self-propelled artillery Company | Self-propelled artillery | 9 | 6 |
| Artillery company | Howitzer | 18 | 12 |
| Anti-tank company | Anti-tank missile vehicle | 9 | 6 |
| Armored reconnaissance battalion | Armored reconnaissance vehicle | 42 | 28 |
Table 2. Reliability degree of materiel in Stryker brigade
| No. | Materiel | Reliability |
|---|---|---|
| 1 | Step vehicle | 0.5259 |
| 2 | Self-propelled artillery | 0.6413 |
| 3 | Howitzer | 0.6825 |
| 4 | Anti-tank missile vehicle | 0.5518 |
| 5 | Armored reconnaissance vehicle | 0.4223 |
4.2. Calculation of Mission Reliability
Table 3. Reliability of equipment systems in Stryker Brigade
| No. | Equipment system | Reliability |
|---|---|---|
| 1 | Infantry company 1-9 | 0.9490 |
| 2 | Self-propelled artillery Company | 0.9870 |
| 3 | Artillery company | 0.9995 |
| 4 | Anti-tank company | 0.9514 |
| 5 | Armored reconnaissance battalion | 0.9086 |
Then, we calculate the reliability of ESoS from the following three ideas.
(1) Model the reliability structure of ESoS as a series system that does not allow any system to fail. ESoS reliability can be obtained from Equation(1):
(2) Model the reliability structure of ESoS as a parallel system composed of different units. ESoS reliability can be obtained from Equation(2):
(3) Model the reliability structure of ESoS as a weighted parallel structure whose reliability model is expressed by Equations(9) and (10).
Through the Delphi method proposed in Section 3.2(2), assume that the reliability normalized weights of each system have been obtained, as shown in Table 4. From Equations(9), (10), and (13), we have
Table 4. Reliability weight of equipment systems
| No. | Equipment system | Reliability weight |
|---|---|---|
| 1 | Infantry company 1-9 | 0.0715 |
| 2 | Self-propelled artillery Company | 0.0795 |
| 3 | Artillery company | 0.0895 |
| 4 | Anti-tank company | 0.0860 |
| 5 | Armored reconnaissance battalion | 0.1015 |
4.3. Result Analysis
It can be seen from the reliability values calculated by the three ideas that the SoS reliability logic is too stringent to describe in series, and the parallel structure description is too wide. At this time, the weighted parallel structure can reflect the reliability of ESoS more accurately.
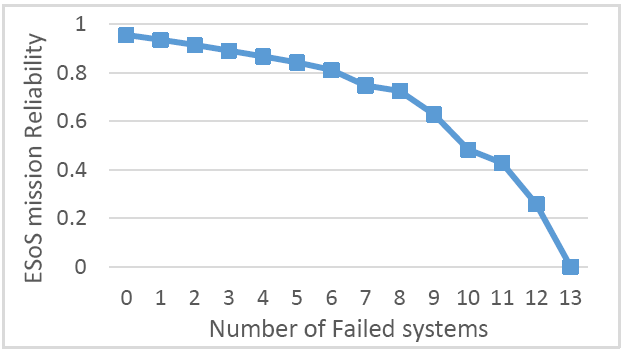
However, a simple reliability value does not indicate the performance degradation process of the equipment system as the system exits. Therefore, consider the change of the ESoS reliability when systems are configured to exit the SoS one by one, as shown in Figure 6.
Figure 6.
Figure 6.
ESoS mission reliability when systems failed progressively
It can be seen from Figure 6 that:
(1) As systems fail and exit from the SoS one by one, the SoS mission reliability is gradually reduced.
(2) As the number of failed systems increases, the slope of the mission reliability curve increases; that is, the rate of decline in mission reliability of the overall SoS increases, which reflects the emergence character of SoS.
(3) The reduction in SoS mission reliability caused by different system failures is different.
5. Conclusions
Based on the mission reliability of ESoS, this paper proposes a calculation method based on the weighted parallel structure to analyze and evaluate the reliability of the ESoS scientifically and rationally and provide a theoretical basis for the evaluation of support capability. The main conclusions and deficiencies of this article are:
(1) Component systems of SoS exit after failure, the SoS performance will decline to some extent, and it is not an absolute state of good or failure. The traditional basic logic structure cannot accurately describe this feature.
(2) The weighted parallel structure can determine the weight by the contribution of the system to SoS and then distribute the SoS reliability. Thus, it can accurately describe the characteristics of SoS.
(3) There is no careful consideration of the impact of complex mission profiles, maintenance support factors, and interactions between systems on the SoS reliability during the discussion of this article, and this needs to be improved in following studies.
Reference
“The Smooth Structure of the Moduli Space of a Weighted Series-Parallel Graph, ”
DOI:10.1016/j.topol.2014.01.012
URL
[Cited within: 1]

Given a weighted graph (G, l) and its associated moduli space M(G, l), then a sufficient condition is provided which ensures that M(G, l) is a smooth manifold whenever G is a series-parallel graph.
“Research on Phased-Mission Success Probability Assessment under Random Common Cause Failures, ”
“Reliability Analysis Method of Phased-Mission Systems with Common Cause Failure based on BDD, ”
“Availability Evaluation Model for the Heterogeneous System based on RBD, ”
“Reliability and Availability Assessment of Seabed Storage Tanks using Fault Tree Analysis, ”
DOI:10.1016/j.oceaneng.2016.04.021
URL
[Cited within: 1]

61The concept of subsea production system with seabed storage tank (SST) was proposed.61The reliability assessment for the SST was estimated using a fault tree analysis.61The repair time for SST was estimated in accordance with MIL-HDBK 472 Procedure V.61Consequently, the availability of the SST was approximately 91.8%.
“Reliability Analysis using a Parallel Evolutionary Algorithm, ”
DOI:10.1016/j.strusafe.2017.01.001
URL
[Cited within: 1]

This paper presents a parallel evolutionary algorithm to solve reliability problems with accuracy and repeatability of results. The last characteristic is usually overlooked; however, it is critical to the reliability of the calculation method itself. Note that evolutionary algorithms are stochastic processes and may not always generate identical results. The optimisation problem resulting from the first order reliability method is considered with an implicit state function that can include a call to a finite element analysis (FEA). A strategy to handle failures from the transformation of random variables or from the finite element call during the evolution process is explained in detail. Several benchmark tests are studied, including some involving bounded random variables that introduce strong non-linearities in the mapping to standard Gaussian space. In addition, the solutions of 2D and 3D frame problems using the finite element method illustrate the capabilities of the algorithm including the convenience of the algorithm in handling discrete limit state functions. Finally, the ability to obtain similar results after many runs is demonstrated.
“Research and Demonstration on Contribution Evaluation of Weapon Equipment System based on Task-Capability-Structure- Evolution, ”
“Research on Cooperating Support Model of Equipment Support System of Systems based on Complex Network, ”
“Research on Phased Mission based Efficient Reliability Evaluation Algorithm for Equipment System of Systems, ”
DOI:10.3969/j.issn.1001-506X.2016.01.35
URL
[Cited within: 1]

The reliability evaluation for systematic fight mission in real time is an inevitably demand of the future wars.In order to solve the computational problem of the equipment system reliability in real time in the phased mission process, an efficient analytical algorithm based on the k/n(G)redundancy model for reliability evaluation is designed.Through the structural analysis of the equipment system and the mission overview, a binary decision diagram(BDD)model is proposed, which is transformed from the redundant fault tree.As for high computational complexity of the traditional method, a more effective algorithm on the basis of the recursive algorithm is designed.Taking the remote target attack mission of the aviation equipment system for instance, the simulation results indicate that the effective results of the phased mission reliability are obtained by using the proposed method.And the results show that the computational efficiency of the proposed algorithm is significantly improved compared with the traditional algorithm.It is applicable for the computational analysis of reliability of the large-scale systematic fight mission in real time and further direct mission plan.
“Complexities of System of Systems Operational Availability Modeling, ”
in
“Modeling of Information Systems as Systems of Systems Through DSM, ”
in
“Reliability Model and Simulation of Equipment System-of-Systems based on Timing Petri Net, ”