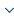1. Introduction
The consecutive-k system was first studied around 1980, and it soon became a very popular subject [1-3].The reasons were many-folded, including: 1. This kind of system is simple and natural, which means that most people can understand it and many can do some analysis. However, it can be developed in many directions, and there is no lack of new topics [4-6]. 2. The consecutive system is simple enough. Thus, it has become a prototype for researchers to demonstrate their various ideas related to reliability theories or applications. For example, the interesting concept of component importance works best with the consecutive-k system [7-9]. 3. The system is supported by many applications. Over the course of nearly forty years, thousands of papers about this subject have been published [2,10-13]. For instance, in reaction to the problems of fixed point measurement of temperature and no measurement of humidity in the current cocoon drying process, a consecutive and dynamic measuring system of cocoon drying temperature and humidity has been developed [14]. The properties of consecutive energy-barrier systems are derived from the basic principles of deformation kinetics and from the rate theory [10]. As the importance and the popularity of the consecutive system keep increasing, its reliability is an important property that should be concerned.
There are some subclasses of the consecutive system. As a generalization of a k-out-of-n: F system, where “F” stands for “fail”, the consecutive k-out-of-n: F system has been studied by many researchers [7, 15-17]. A k-out-of-n: F system has a total of n components and fails if at least k components fail. This type of structure has been widely applied in voting systems, power systems, etc. Different from the k-out-of-n: F system, a consecutive k-out-of-n: F system fails if at least F consecutive components out of the total n components fail [18-19]. This type of structure has applications in telecommunication systems, oil pumping systems, etc. The failure of too many relay stations in the telecommunication system may make the signal transmission disconnected. Following the basic definitions of the two types of systems, some variants or generalizations of them have been studied [20-22]. Habib et al. [23] studied the reliability of a multi-state consecutive k-out-of-r-from-n: G system, where G stands for “good”. This type of system has n components having multiple states and works if there exist kj components out of any r consecutive components above state j for any j. Levitin [24] studied a system consisting of n components, which fails if the gap between any two groups of r consecutive components containing at least k failed components is less than m components. Peng et al. [25] studied the optimal component allocation in a linear multi-state consecutive connected system, of which the consecutive k-out-of-n: F system can be regarded as a special case.
None of them have considered the case where a system may fail if either any consecutive number of components fail or any total number of components fail. For example, the speech recognition system may be deemed as unsuccessful if too many consecutive words are recognized wrongly or the total number of wrongly recognized words is too many. In [26], a model is proposed to consider both failure modes. However, it shows only the iterative relationship, but not the detailed calculation process. In this paper, we consider a system with n linearly arranged components, which fails either when any k consecutive components fail or any v>k arbitrary components fail. The system is termed as a combined consecutive k and v-out-of-n system. The iterative approach proposed is somewhat different from the one in [26]. This paper focuses on the iterative relationship between the success probabilities, whereas [27] obtains the iterative relationship between the failure probabilities. Moreover, numerical examples are presented to show the detailed calculation processes.
The remaining of this paper is as follows. Section 2 elaborates on an iterative approach for evaluating the reliability of such a system. Section 3 provides a numerical example to illustrate the applications. Section 4 presents the conclusions.
Nomenclature
| n | Total numbers of components |
|---|---|
| p | Fault detection process |
| k | The number of the consecutive failed components that lead to the failure of the whole system |
| v | The number of the failed components in arbitrary position that lead to the failure of the whole system |
| $R(n,k,v,p)$ | The reliability of the whole system that have two types of failure modes |
| ${{R}_{C}}(n,k,p)$ | The reliability of the whole system that fails if k consecutive components fail |
| ${{R}_{A}}(n,v,p)$ | The reliability of the whole system that fails if v components in arbitrary positions fail |
| m | The index of the first component that does not fail |
| $Q(m)$ | The probability that the first working component is the No. m in the whole system |
| ${{N}_{C}}(j,k,n-m)$ | The number of ways to arrange j failed components within n-m linearly ordered components under the condition that no k or more failed components are consecutive |
| $j/k$ | The maximum integer no largerthan$j/k$ |
| $C(n,k,v)$ | The complexity of calculating the reliability of a combined consecutive k and v-out-of-n system |
2. The Model
In this study, we consider a combined consecutive k and v-out-of-n system with n linearly arranged homogeneous components, each with failure probability p. The reliability of the whole system is denoted as $R(n,k,v,p)$. The system fails if any $k<n$ consecutive components fail or any $v\text{ }(n>v>k)$ arbitrary components fail. The reliabilities for the two types of failure are indicated by ${{R}_{C}}(n,k,p)$ and ${{R}_{A}}(n,v,p)$ respectively. In order to get the form of $R(n,k,v,p)$, an iterative approach can be adopted. The system and the two types of failures are shown in Figure 1.
Figure 1
Figure 1.
The system and the failure types
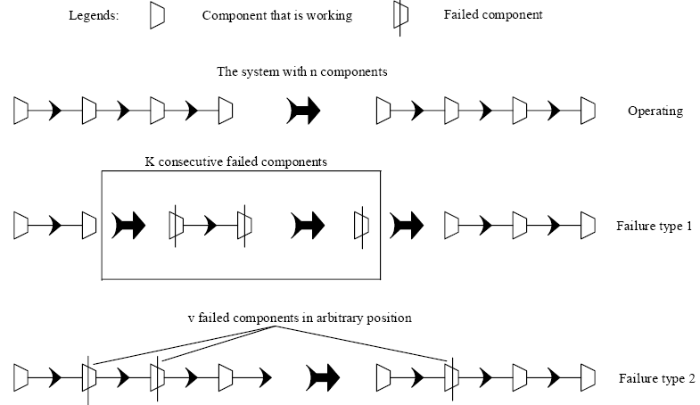
Use m to denote the index of the first component that does not fail. It is easy to see that the system is possible to function only when m ≤ k. The probability associated with each m can be calculated as
This can be illustrated in Figure 2. For each realization of m, the conditional probability that the system functions can be denoted as $R(n-m,k,v-m+1,p)$. Furthermore, the system reliability can be obtained as
Figure 2
Figure 2.
Two failure types
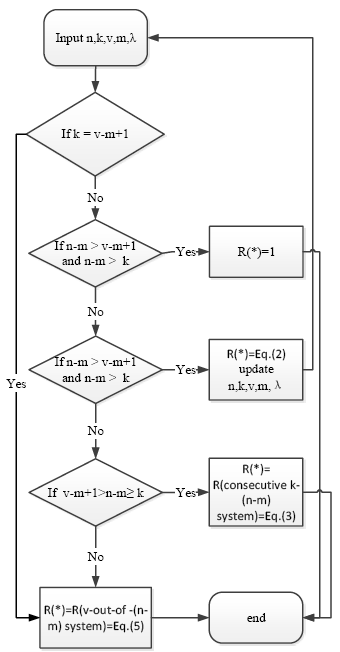
In order to calculate $R(n-m,k,v-m+1,p)$, we need to distinguish a few cases based on the values of ($n-m$), k, and ($v-m+1$).In detail,if($n-m$) becomes smaller than both k and ($v-m+1$), this means the components left that may fail are less than the minimum number of the failed components that lead to the failure of the whole system. In this case, $R(n-m,k,v-m+1,p)$ equals 1.Otherwise, we should first determine whether the k is equal to($v-m+1$). If k is equal to ($v-m+1$), $R(n-m,k,v-m+1,p)$ becomes a k-out-of-(n-m) system where the system fails if any k arbitrary components fail. In the cases where the values of k and ($v-m+1$) are different and the ($n-m$)lies between k and ($v-m+1$), the system becomes either a consecutive [$k-(n-m)$] system or a v-out-of-(n-m) system. In either case, the form of $R(n-m,k,v-m+1,p)$ can be obtained. Finally, for the case where ($n-m$) is no smaller than both ($v-m+1$)and k, we still need to use the iterative approach.
The mathematical expressions for these cases are shown as follows:
$R(n-m,k,v-m+1,p)=1$,
if $n-m<k\text{ }\!\!\And\!\!\text{ }n-m<v-m+1$;
$R(n-m,k,v-m+1,p)={{R}_{C}}(n-m,k,p)$,
if $v-m+1>n-m\ge k$;
$R(n-m,k,v-m+1,p)={{R}_{A}}(n-m,v-m+1,p)$,
if $n-m\ge v-m+1\text{ }\!\!\And\!\!\text{ }k\ge v-m+1$;
$R(n-m,k,v-m+1,p)=\sum\nolimits_{1\le {m}'\le k}{Q({m}')R(n-m-{m}',k,v-m+1-{m}',p)}$,
if $n-m\ge k\text{ }\!\!\And\!\!\text{ }n-m\ge v-m+1\text{ }\!\!\And\!\!\text{ }k<v-m+1$.
For case (2), the system consisting of the last (n-m)components degenerates to a simple consecutive k-out-of-(n-m) system, the reliability of which can be calculated using the next formula:
Where ${{N}_{C}}(j,k,n-m)$ denotes the number of ways to arrange j failed components within (n-m) linearly ordered components under the condition that no k or more failed components are consecutive. ${{N}_{C}}(j,k,n-m)$is given as follows [12]:
Where $j/k$ denotes the maximum integer no largerthan $j/k$.
For case (3), the system consisting of the last n-m components degenerates to a simple (v-m+1)-out-of-(n-m) system, the reliability of which can be calculated using the next formula:
Where $C_{n-m}^{j}$ denotes the number of ways to arrange j failed components within (n-m) linearly ordered components in arbitrary position.
For case (4), the iteration process will be repeated again from the start. The whole process is shown in Figure 3.
Figure 3
Figure 3.
The flow chart for the calculation process of $R(n-m,k,v-m+1,p)$
Then, to determine the computational complexity of the system reliability, we can perform the complexity analysis for the reliability calculation. If the reliability of a system can be calculated directly without using Equation (2), we define the complexity in this case as 1 degree. The total complexity is obtained by the sum of the complexities of the systems that degenerate according to Equation (2).
We use $C(n,k,v)$ to represent the complexity of calculating the reliability of a combined consecutivek and v-out-of-n system. It can be calculated as follows:
3. Numerical Example
3.1. Example 1
In this section, a specific model configuration is shown for illustration. It is assumed that there are a total of two different kinds of debuggers. The simulation process is briefly described in the following flow chart:
Consider a system consisting of n=5 homogeneous components, each with failure probability p=0.1. The system fails if at least k=2 consecutive components fail or any three arbitrary components fail. The reliability of the system can be denotedas $R(5,2,3,0.1)$.
According to (2), we have
From(1), it can be calculated that Q(1)=0.9 and Q(2)=0.09. Thus, we have
Note that $R(4,2,3,0.1)$ belongs to case 4 discussed in section 2, and thus it should be further decomposed. Differently, $R(3,2,2,0.1)$ belongs to case(3) discussedin section 2, and it degenerates to ${{R}_{A}}(3,2,0.1)$. We first calculate ${{R}_{A}}(3,2,0.1)$. According to (5), we have
In addition, according to (2), we have
Furthermore, as Q(1)=0.9 and Q(2)=0.09, we have
It can be seen that $R(3,2,3,0.1)$ belongs to case(4) discussed in section 2. $R(2,2,2,0.1)$ belongs to case(3) discussed in section 2. It is easy to see that
Thus, we only need to calculate $R(3,2,3,0.1)$. According to (2), we have
Note that $R(2,2,3,0.1)$ belongs to case 2 discussed in section 2, and it degenerates to ${{R}_{C}}(2,2,0.1)$, which equals 0.99. On the other hand,$R(1,2,2,0.1)$ belongs to case 1 discussed in section 2, which equals 1. Thus, we have
Substituting (14) and (16) into (13), it can be obtained that
Substituting (12) and (13) into (6) gives
Thus, the system reliability is 0.96228.
The complexity of this example can be calculated as the following process:
3.2. Example 2
Consider a system consisting of n= 6 homogeneous components, each with failure probability p=0.1. The system fails if at least k= 3consecutive components fail or any four arbitrary components fail. The reliability of the system can be denotedas $R(6,3,4,0.2)$.
According to (2), we have
From (1), it can be calculated that Q(1)=0.8, Q(2)=0.16, and Q(3)=0.032. Thus, we have
Note that $R(5,3,4,0.2)$ belongs to case 4 discussed in section 2, and thus it should be further decomposed. Differently, $R(4,3,3,0.2)$ and $R(3,3,2,0.2)$ belong to case(3) discussedin section 2 and degenerate to ${{R}_{A}}(4,3,0.2)$ and ${{R}_{A}}(3,2,0.2)$ respectively. We first calculate $R(4,3,3,0.2)$ and $R(3,3,2,0.2)$. According to (3), we have
In addition, according to (2), we have
Similarly, as Q(1)=0.8, Q(2)=0.16, andQ(3)=0.032, we have
$R(3,3,3,0.2)$ and $R(2,3,2,0.2)$ belong to case(3) discussedin section 2, so they can degenerate to ${{R}_{A}}(3,3,0.2)$ and ${{R}_{A}}(2,2,0.2)$ respectively. We first calculate $R(3,3,3,0.2)$ and $R(2,3,2,0.2)$. According to (3), we have
For $R(4,3,4,0.2)$, it can continue to be decomposed according to Equation (2), as shown below:
$R(2,3,3,0.2)$ and $R(1,3,2,0.2)$ are directly equal to 1 according to the condition in case (1). $R(3,3,4,0.2)$ degenerates to ${{R}_{C}}(3,3,0.2)$ as shown in case (2), and it can be easily calculated as
Then, we can calculate the reliability of the whole system as the following process:
Thus, the reliability for this example is 0.966528.
The complexity of this example can be calculated as the following process:
4. Sensitivity Analysis
To investigate how the variation of the related parameters would influence the reliability of the system, the sensitivity analysis was conducted. We varied the values of k, v, and p to see how the reliability changes.
Table 1 shows the variations of the system reliability for different k. It is noted that the reliability of the system increases monotonically with k, which can be interpreted as that the system tends to be less prone to failure as the failure condition becomes rigorous. Especially when k = 1, the reliability is only about 0.59, which means the system is no longer a consecutive k-out-of-n system. This can largely influence the reliability.
Table 1. Variations of the reliability for different k when n=5, v=3, and p=0.1
| k | $R(5,k,3,0.1)$ |
|---|---|
| 1 | 0.59045 |
| 2 | 0.96228 |
| 3 | 0.99104 |
Table 2 presents the influence of the v on the system reliability. It can be seen that with an increase inv, the reliability of the whole system also increases. In this case, the number of failed components needed is increasing, which means the failure condition of the whole system also becomes rigorous.As a result, the reliability increases with an increase in v.
Table 2. Variations of the reliability for different v when n=5, k=2, and p=0.1
| v | $R(5,2,v,0.1)$ |
|---|---|
| 1 | 0.91845 |
| 2 | 0.96228 |
| 3 | 0.96309 |
Anopposite situation happens when considering the influence of failure probability for a single component on the system reliability. Table 3 shows the variations of the reliability for different p. The bigger p represents that the component is more likely to fail, which can increase the failure probability of the whole system. Thus, the reliability of the system is negatively correlated with the failure probability of its components.
Table 3. Variations of the reliability for different p when n=5, k=2, and v=3
| p | $R(5,2,3,p)$ |
|---|---|
| 0.1 | 0.96228 |
| 0.2 | 0.88704 |
| 0.5 | 0.495 |
| 0.8 | 0.103 |
In summary, the reliability of the system is positively associated with the minimum required quantities of the consecutive components and of the components in arbitrary position but negatively correlated with the failure probability of its components.
5. Conclusions
This paper considers a system that fails either due to the failure of too many components or too many consecutive components. An iterative approach has been proposed to calculate the system reliability. Different from previous research, which focused on the iterative relationship between the failure probabilities, this paper focuses on the iterative relationship between the success probabilities. Numerical examples are proposed for illustrative purposes. In the future, this work can be extended to the case where each component has more than two states.
Acknowledgements
This research was partially supported by the NSFC(No. 71671016, 71231001) and the Fundamental Research Fund of Central Universities (No. FRF-GF-17-B14).
Reference
Reliability of Consecutive-k-out-of-n: F System
,”
DOI:10.1109/TR.1981.5220981
URL
[Cited within: 1]

A reliability diagram with n components in sequence is called consecutive-k-out-of-n:F system if the system fails whenever k consecutive components are failed. This paper presents a recursive formula to compute the exact system reliability, and gives sharp upper and lower bounds for it.
Reliabilities of Consecutive-k Systems
”
DOI:10.1007/1-85233-841-5_3
URL
[Cited within: 1]

The consecutive-k system was first studied around 1980, and it soon became a very popular subject. The reasons were many-folded, includ ing: 1. The system is simple and natural. So most people can understand it and many can do some analysis. Yet it can grow in many directions and there is no lack of new topics. 2. The system is simple enough to become a prototype for demonstrat ing various ideas related to reliability. For example, the interesting concept of component importance works best with the consecutive-k system. 3. The system is supported by many applications. Twenty years have gone and hundreds of papers have been published on the subject. This seems to be a good time for retrospect and to sort the scattered material into a book. Besides providing our own per spective, the book will also serve as an easy reference to the numerous ramifications of the subject. It is hoped that a summary of work in the current period will become the seed of future break-through.
On the Consecutive-k-of-n: F System
,”
DOI:10.1109/TR.1982.5221229
[Cited within: 1]

The linear (circular) k-of-n:F system has n linearly (circularly) ordered components. Each component either functions or fails. The system fails i.f.f.k consecutive components fail. This paper provides, in the i.i.d. case, recursive formulas and bounds for computing system reliability. It considers properties of system life distributions and, in the non i.i.d. case, questions of optimal system design.
Design of Consecutive Compensator for Servo System with Signal Uncertainty
,” in
DOI:10.1007/978-3-319-65960-2_8
URL
[Cited within: 1]

Results of the research of signal uncertainty problem are presented. The problem arises during design of consecutive compensator for a servo system. The problem is solved using Besekersky approach. Th
Reliability of Linear Consecutive-k-out-of-n Systems with Two Change Points
,”
DOI:10.1109/TR.2018.2829709
URL

Linear consecutive-k-out-of-n systems are frequently used to model vacuum systems, telecommunication networks, oil pipeline systems, and the photographing of nuclear accelerators. Substantial research has been devoted to analyzing the reliability of such systems, using many different approaches and assumptions. Nevertheless, existing reliability formulas may not be suitable for all real systems. This paper therefore proposes a nonrecursive closed-form expression for a consecutive-k-out-of-n system that is made up of three types of nonidentical components. The corresponding dynamic survival function and mean time to failure are derived for the suggested system, and numerical experiments are carried out to illustrate its application.
Reliability of Phase Mission Linear Consecutively-Connected Systems with Constrained Number of Consecutive Gaps
,” in
DOI:10.1109/ICSRS.2016.7815854
URL
[Cited within: 1]

There are many linear consecutive connected systems with multi-phase missions, such as the modem water diversion system. In each phase, they can be treated as a linear consecutively-connected system (LCCS), and the whole system with multi-phase missions can be modelled as the phase mission linear consecutive connected system (PM-LCCS). With the development of bypass transportation system, every phase allows a limited number of consecutive disconnections betw een nodes which can also be referred as gaps. We generalized the traditional PM-LCCS model with the M consecutive gaps in each phase mission. In the proposed model, if the number of consecutive gaps in a phase mission exceeds the limitation M, the phase mission will fail; and the failure of any phase can cause the failure of the whole system A recursive algorithm is adopted to analyze the system reliability. At last, the proposed model is implemented by an illustrative example.
Optimization of Linear Consecutive-k-out-of-n System with a Birnbaum Importance-based Genetic Algorithm
,”
DOI:10.1016/j.ress.2016.03.016
URL
[Cited within: 2]

61BIGA integrates BI and GA to solve the Lin/Con/k/nsystems optimization problems.61The experiment results show that the BIGA performs well in most conditions.61Suggestions are given for the application of BIGA and BITA with differentkandn.61The application procedure of BIGA is demonstrated by the oil transportation system.
Reliability and Joint Reliability Importance in a Consecutive-k-within-m-out-of-n: F System with Markov-Dependent Components
,”
DOI:10.1109/TR.2015.2484079
URL

This paper studies a consecutive- k-within- m-out- of- n:F system with Markov-dependent components; that is, the reliability of a component depends on its neighbors. Using probability generating functions, the closed-form formula for reliability of the consecutive- k-within- m-out-of- n:F system with Markov-dependent components and a closed-form formula for joint reliability importance (JRI) of two components in such a system are derived. The JRI of two components evaluates the interaction effect between the components on contributing to system reliability. A formula of the JRI of more than two components are also derived and presented. Many real systems and procedures, such as radar detection systems, pipeline systems, quality inspection procedures, and so on, can be modeled as a consecutive- k-within- m-out-of- n:F system, in which components are Markov-dependent. The present results can evaluate the reliability of these systems or the accuracy of the procedures as well as the contributions of components to the system reliability or the accuracy of the procedures. The applications of the present formulas are demonstrated through the numerical examples. The examples show the changes of system radiabilities and the changes among the JRI values of different pairs of components in consecutive- k-within- m-out-of- n:F systems. The JRI values of Markov-dependent components are also compared to the JRI values of s-independent components.
Reliability and Importance Measures for m-Consecutive-k, l-out-of-n System with Non-Homogeneous Markov-Dependent Components
,”
Properties of Consecutive Energy Barriers and the Associated Behavior in Plastic Flow
,”
DOI:10.1063/1.325404
URL
[Cited within: 2]

The properties of consecutive energy‐barrier systems are derived from the basic principles of deformation kinetics and from the rate theory as applied to plastic flow. It is shown that these properties are functions of well‐defined relations between the activation energy and volumes of the different barriers. In particular, for a system of two consecutive energy barriers, it is shown that the usual equation used to calculate the strain rate ?=ε0/(t1+t2), wheret1andt2are two waiting times, is only an approximation valid when backward activations are negligible. The behavior of materials, in which plastic flow is controlled by a system of two consecutive energy barriers, was determined rigorously for various experimental conditions. It is shown that the calculated temperature dependence of the flow stress as well as the stress and temperature dependence of the experimental activation volume and strain‐rate sensitivity that follow from the properties of consecutive energy barriers are in agreement with experimental observations.
A Consecutive k-out-of-n Reliability System in Random Environment
,”
DOI:10.1016/0026-2714(94)90144-9
URL

Linear and circular consecutive k-out-of-n reliability system are assumed to be situated in a random environment such that shocks generated by the environment will cause failure with probability p to one randomly chosen component. Explicit formulas for k = 2 and 3 are derived for generating functions and expectations and variances for the system time to failure. An equivalene between linear and circular systems is derived.
Consecutive-Type Reliability Systems: An Overview and Some Applications,”
Application and Analysis for a Consecutive-k-out-of-n: G Structure
,”
DOI:10.1016/0951-8320(91)90058-F
URL
[Cited within: 1]

A consecutive- k -out-of- n :G system consists of an ordered sequence of n components such that the system works whenever at least k consecutive components in the system function. This study elaborates on the concept of consecutive- k -out-of- n:G systems and demonstrates an application of the basic theory of consecutive- k -out-of- n:G systems reliability to a railroad operation. The results can help in scheduling the incoming trains to utilize the station resources better.
Consecutive and Dynamic Measuring System of Cocoon Drying Temperature and Humidity and its Practical Application
,”In reaction to the problems of fixed point measurement of temperature and no measurement of humidity in current cocoon drying process,a consecutive and dynamic measuring system of cocoon drying temperature and humidity has been developed,with which the temperature and humidity of gas in the CL-100 Hot-air Circulating Cocoon Dryer is measured practically to analyze the changes of temperature and humidity inside the cocoon dryer.The results indicate that the system is completely suitable for the measurement of temperature and humidity in cocoon dryers and its application will help to formulate proper cocoon drying process and improve the cocoon drying quality.
Reliability Properties of Consecutive k-out-of-n Systems of Arbitrarily Dependent Components
,”
DOI:10.1016/j.ress.2008.03.027
URL
[Cited within: 1]

In this paper, the reliability properties of consecutive k-out-of- n systems with arbitrarily dependent components are studied. For 2 k 82 n we present efficient formulas to compute the reliability characteristics such as meantime to failure, failure rate, and mean residual lifetime. Approximations for the survival functions when 1 81 k 81 n are also provided. The results are illustrated for the multivariate survival distribution generated by a Weibull and Inverse-Gaussian mixture.
El-Sayed, “Consecutive k-out-of-n: F System with Sequential Failures and a Single Repair
,”
New Bounds on the Reliability of the Consecutive k-out-of-r-from-n: F System
,”
DOI:10.1016/S0951-8320(99)00021-6
URL
[Cited within: 1]

The main goal of this article is to show that the lower and upper bounds on the failing probability resp. reliability of consecutive k-out-of- r-from- n: F reliability systems developed by Sfakianakis, Kounias and Hillaris [M. Sfakianakis, S. Kounias, A. Hillaris, IEEE Trans. Reliability 1992;R-41:442–447] can be improved by applying fourth order Boole–Bonferroni bounds. Further we propose the application of the Hunter–Worsley bound in the framework of reliability system analysis, too. Numerical results of the formerly published test examples and harder problems are given. The computer code was written in Fortran and is available on request from the authors.
Optimal Arrangement of Components in a Consecutive k-out-of-r-from n: F System
,”
DOI:10.1016/0026-2714(93)90111-B
URL
[Cited within: 1]

A consecutive k-out-of-r-from n:F system is an ordered linear arrangement of n components that fails if and only if at least k in a “window” of r consecutive components fail. Suppose that all components are interchangeable and that component failures are s-independent. Component failure probabilities need not be equal. In this paper the ordering of the components in order to minimize the probability of system failure is examined. All values of k,r,n for which an optimal configuration can be determined, without knowledge of the component failure probabilities, are given.
Connectivity Modeling and Optimization of Linear Consecutively Connected Systems with Repairable Connecting Elements
,”
DOI:10.1016/j.ejor.2017.06.047
URL
[Cited within: 1]

Linear consecutively connected systems (LCCSs) are systems containing a linear sequence of ordered nodes. Connection elements (CE) characterized by diverse connection ranges, time-to-failure and time-to-repair distributions are allocated to different nodes to provide the system connectivity, i.e., a connection between the source and sink nodes of the LCCS. Examples of LCCSs abound in practical applications such as flow transmission systems and radio communication systems. Considerable research efforts have been expended in modeling and optimizing LCCSs. However, most of the existing works have assumed that CEs either are non-repairable or undergo a restrictive minimal repair policy with constant repair time. This paper makes new technical contributions by modeling and optimizing LCCSs with CEs under corrective maintenance with random repair time and different repair policies (minimal, perfect, and imperfect). The characteristics of CEs can depend on their location because the distance between adjacent nodes and conditions of CE operation and maintenance at different nodes can be different, which further complicates the problem. We first propose a discrete numerical algorithm to evaluate the instantaneous availability of each CE. A universal generating function based method is then implemented for assessing instantaneous and expected system connectivity for a specific CE allocation. As the CE allocation can have significant impacts on the system connectivity, we further define and solve the optimal CE allocation problem, whose objective is to find the CE allocation among LCCS nodes maximizing the expected system connectivity over a given mission time. Effects of different parameters including repair efficiency, mission time and repair time are investigated. As illustrated through examples, optimization results can facilitate optimal decisions on robust design and effective operation and maintenance managements of LCCSs.
Linear Consecutive-k-out-of-n: F System Reliability with Common-Mode Forced Outages
,”
DOI:10.1016/0951-8320(93)90017-S
URL
[Cited within: 1]

This paper presents a model of consecutive-k-out-of-n: F system subject to common-mode forced outages, whose interarrival times are independent and exponentially distributed. The objective is to analytically derive the mean operating time between failures for a non-repairable component system. The average system failure time and the system availability are also considered. Then, the model is extended to a system with repairable components and unrestricted repair, in which service times are exponentially distributed.
Efficient Analysis of Multi-state k-out-of-n Systems
,”
DOI:10.1016/j.ress.2014.09.006
URL

61We analyze multi-state k-out-of-n systems with independent, non-identical components.61A new analytical method based on multi-valued decision diagram (MDD) is proposed.61MDD-based method fully makes use of the well-defined k-out-of-n structure.61MDD-based method offers lower computational complexity than the recursive algorithms.
Reliability of Multistate Consecutively-Connected Systems
,”
DOI:10.1016/0951-8320(94)90009-4
URL
[Cited within: 1]

ABSTRACT A system consists of an ordered sequence of n failure-prone components which all have the same transmitting capability k. The system is generalized to the consecutively-connected system in which each component may have a different transmitting capability. In a multistate consecutively-connected system, a component may have more than two states (working and failed). This paper provides an efficient algorithm for reliability evaluation of a circular multistate consecutively-connected system. An example is included to illustrate the application of the algorithm developed.
Reliability Evaluation of Multi-state Consecutive k-out-of-r-from-n: G System
,”
DOI:10.1016/j.apm.2006.09.006
URL
[Cited within: 1]

This paper proposes a model that generalizes the linear consecutive k-out-of- r-from- n: G system to multi-state case. In this model the system consists of n linearly ordered multi-state components. Both the system and its components can have different states: from complete failure up to perfect functioning. The system is in state j or above if and only if at least k j components out of r consecutive are in state j or above. An algorithm is provided for evaluating reliability of a special case of multi-state consecutive k-out-of- r-from- n: G system. The algorithm is based on the application of the total probability theorem and on the application of a special case taken from the [Jinsheng Huang, Ming J. Zuo, Member IEEE and Yanhong Wu, Generalized multi-state k-out-of- n: G system, IEEE Trans. Reliab. 49(1) (2000) 105 111.]. Also numerical results of the formerly published test examples and new examples are given.
Linear m-Gap-Consecutive k-out-of-r-from-n: F Systems
,”
Element Maintenance and Allocation for Linear Consecutively Connected Systems
,”
DOI:10.1080/0740817X.2011.649388
URL
[Cited within: 1]

This article considers optimal maintenance and allocation of elements in a Linear Multi-state Consecutively Connected System (LMCCS), which is important in signal transmission and other network systems. The system consists of N+1 linearly ordered positions (nodes) and fails if the first node (source) is not connected with the final node (sink). The reliability of an LMCCS has been studied in the past but has been restricted to the case when each system element has a constant reliability. In practice, system elements usually fail with increasing failure probability due to aging effects. Furthermore, in order to increase system availability, resources can be put into the maintenance of each element to increase the availability of the element. In this article, a framework is proposed to solve the cost optimal maintenance and allocation strategy of this type of system subject to an availability requirement. A universal generating function is used to estimate the availability of the system. A genetic algorithm is adopted for optimization. Illustrative examples are presented.
Reliability Evaluation of Combined k-out-of-n:F, Consecutive-k-out-of-n: F and Linear Connected-(r, s)-out-of--(m, n): F System Structures
,”
DOI:10.1109/24.855542
URL
[Cited within: 2]

). The algorithms are used for system reliability evaluation of furnace systems. The concept of the combined k-out-of-n:F and 1-dimensional and 2-dimensional consecutive-k-out-of-n:F systems can be extended to other variations of the consecutive-k-out-of-n:F systems, e.g., the consecutive-k-out-of-n:G system and 1-dimensional and 2-dimensional r-within-k-out-of-n:F systems. The concept of Markov chain imbeddable (MIS) systems is another excellent tool that can be used for analysis of such combined system structures